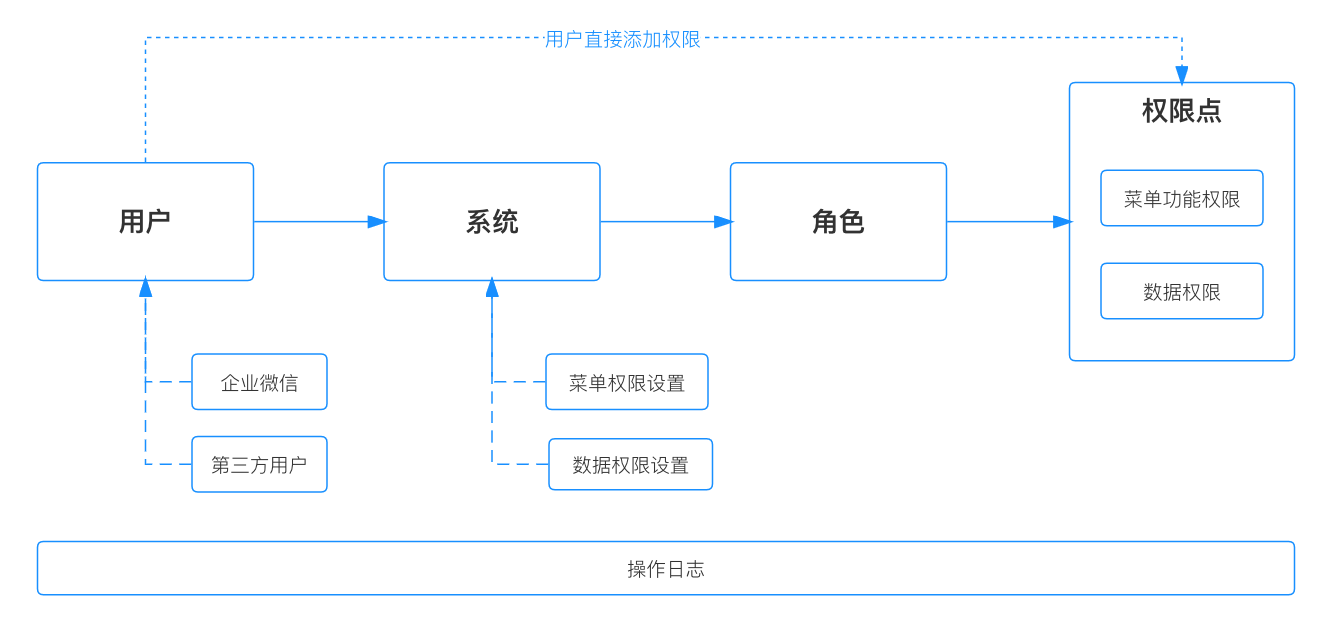
什么是内存碎片?
你可以将内存碎片简单地理解为那些不可用的空闲内存。
举个例子:操作系统为你分配了 32 字节的连续内存空间,而你存储数据实际只需要使用 24 字节内存空间,那这多余出来的 8 字节内存空间如果后续没办法再被分配存储其他数据的话,就可以被称为内存碎片。
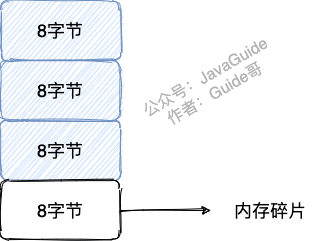
Redis 内存碎片虽然不会影响 Redis 性能,但是会增加内存消耗。
为什么会有 Redis 内存碎片?
Redis 内存碎片产生比较常见的 2 个原因:
1、Redis 存储数据的时候向操作系统申请的内存空间可能会大于数据实际需要的存储空间。
以下是这段 Redis 官方的原话:
To store user keys, Redis allocates at most as much memory as the
maxmemorysetting enables (however there are small extra allocations possible).
Redis 使用 zmalloc 方法(Redis 自己实现的内存分配方法)进行内存分配的时候,除了要分配 size 大小的内存之外,还会多分配 PREFIX_SIZE 大小的内存。
zmalloc 方法源码如下(源码地址:https://github.com/antirez/redis-tools/blob/master/zmalloc.c):
1 | void *zmalloc(size_t size) { |
另外,Redis 可以使用多种内存分配器来分配内存( libc、jemalloc、tcmalloc),默认使用 jemalloc,而 jemalloc 按照一系列固定的大小(8 字节、16 字节、32 字节……)来分配内存的。jemalloc 划分的内存单元如下图所示:
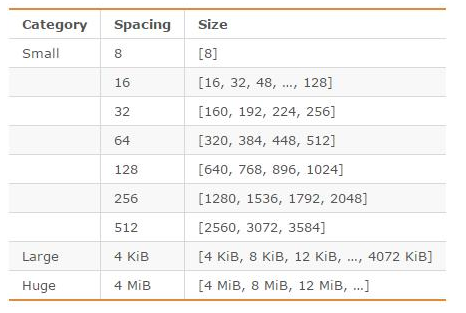
当程序申请的内存最接近某个固定值时,jemalloc 会给它分配相应大小的空间,就比如说程序需要申请 17 字节的内存,jemalloc 会直接给它分配 32 字节的内存,这样会导致有 15 字节内存的浪费。不过,jemalloc 专门针对内存碎片问题做了优化,一般不会存在过度碎片化的问题。
2、频繁修改 Redis 中的数据也会产生内存碎片。
当 Redis 中的某个数据删除时,Redis 通常不会轻易释放内存给操作系统。
这个在 Redis 官方文档中也有对应的原话:

文档地址:https://redis.io/topics/memory-optimization 。
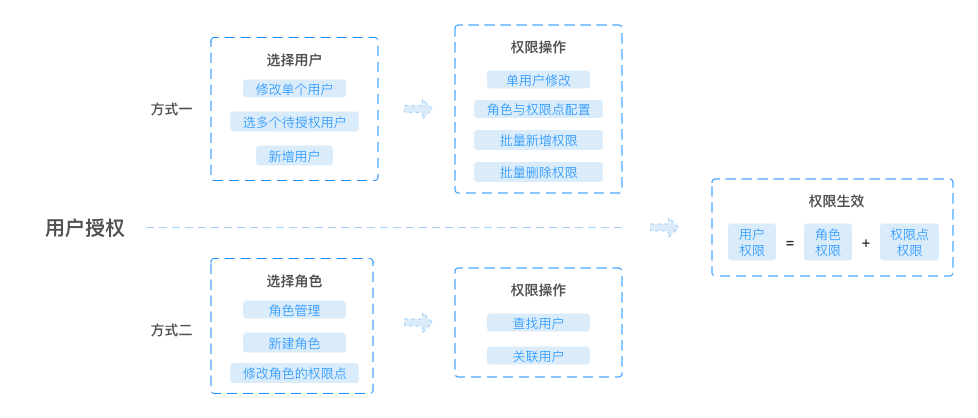
如何查看 Redis 内存碎片的信息?
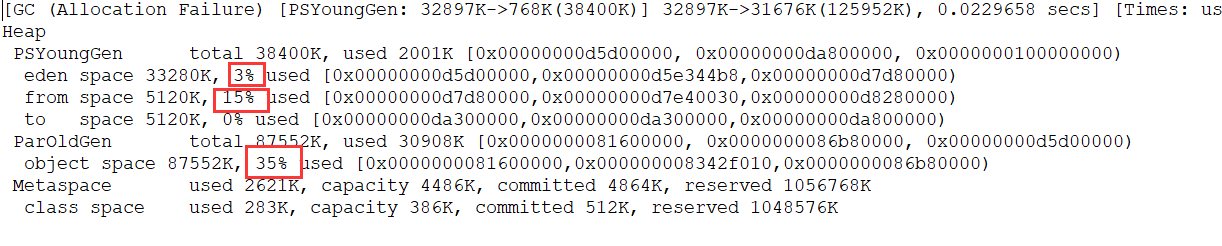
使用 info memory 命令即可查看 Redis 内存相关的信息。下图中每个参数具体的含义,Redis 官方文档有详细的介绍:https://redis.io/commands/INFO 。
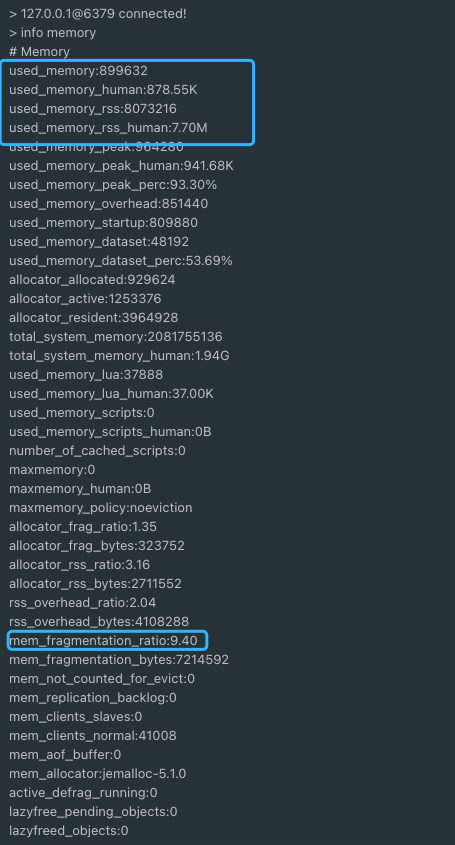
Redis 内存碎片率的计算公式:mem_fragmentation_ratio (内存碎片率)= used_memory_rss (操作系统实际分配给 Redis 的物理内存空间大小)/ used_memory(Redis 内存分配器为了存储数据实际申请使用的内存空间大小)
也就是说,mem_fragmentation_ratio (内存碎片率)的值越大代表内存碎片率越严重。
一定不要误认为used_memory_rss 减去 used_memory值就是内存碎片的大小!!!这不仅包括内存碎片,还包括其他进程开销,以及共享库、堆栈等的开销。
很多小伙伴可能要问了:“多大的内存碎片率才是需要清理呢?”。
通常情况下,我们认为 mem_fragmentation_ratio > 1.5 的话才需要清理内存碎片。 mem_fragmentation_ratio > 1.5 意味着你使用 Redis 存储实际大小 2G 的数据需要使用大于 3G 的内存。
如果想要快速查看内存碎片率的话,你还可以通过下面这个命令:
1 | > redis-cli -p 6379 info | grep mem_fragmentation_ratio |
另外,内存碎片率可能存在小于 1 的情况。这种情况我在日常使用中还没有遇到过,感兴趣的小伙伴可以看看这篇文章 故障分析 | Redis 内存碎片率太低该怎么办?- 爱可生开源社区 。
如何清理 Redis 内存碎片?
Redis4.0-RC3 版本以后自带了内存整理,可以避免内存碎片率过大的问题。
直接通过 config set 命令将 activedefrag 配置项设置为 yes 即可。
1 | config set activedefrag yes |
具体什么时候清理需要通过下面两个参数控制:
1 | # 内存碎片占用空间达到 500mb 的时候开始清理 |
通过 Redis 自动内存碎片清理机制可能会对 Redis 的性能产生影响,我们可以通过下面两个参数来减少对 Redis 性能的影响:
1 | # 内存碎片清理所占用 CPU 时间的比例不低于 20% |
另外,重启节点可以做到内存碎片重新整理。如果你采用的是高可用架构的 Redis 集群的话,你可以将碎片率过高的主节点转换为从节点,以便进行安全重启。
参考
- Redis 官方文档:https://redis.io/topics/memory-optimization
- Redis 核心技术与实战 - 极客时间 - 删除数据后,为什么内存占用率还是很高?:https://time.geekbang.org/column/article/289140
- Redis 源码解析——内存分配:<https://shinerio.cc/2020/05/17/redis/Redis 源码解析——内存管理>
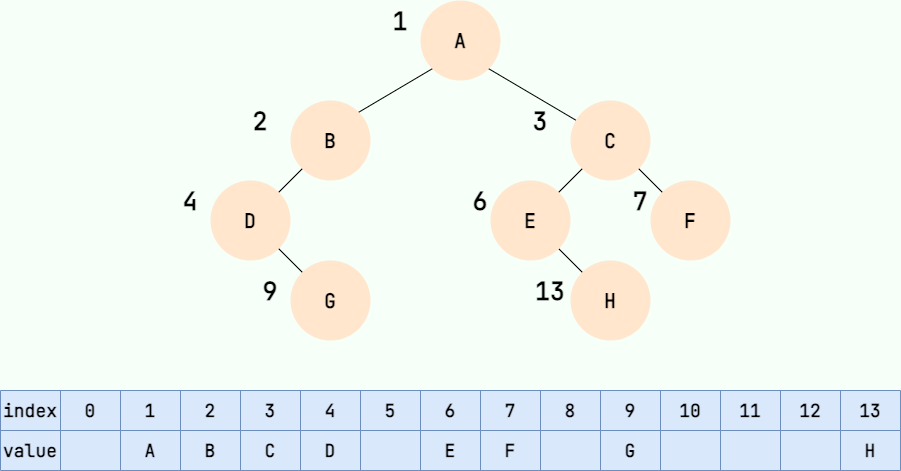
 循环不变式是:
循环不变式是: